1. Delta function

We first introduce some important functions: Delta function, Step function, Ramp function, Square function.

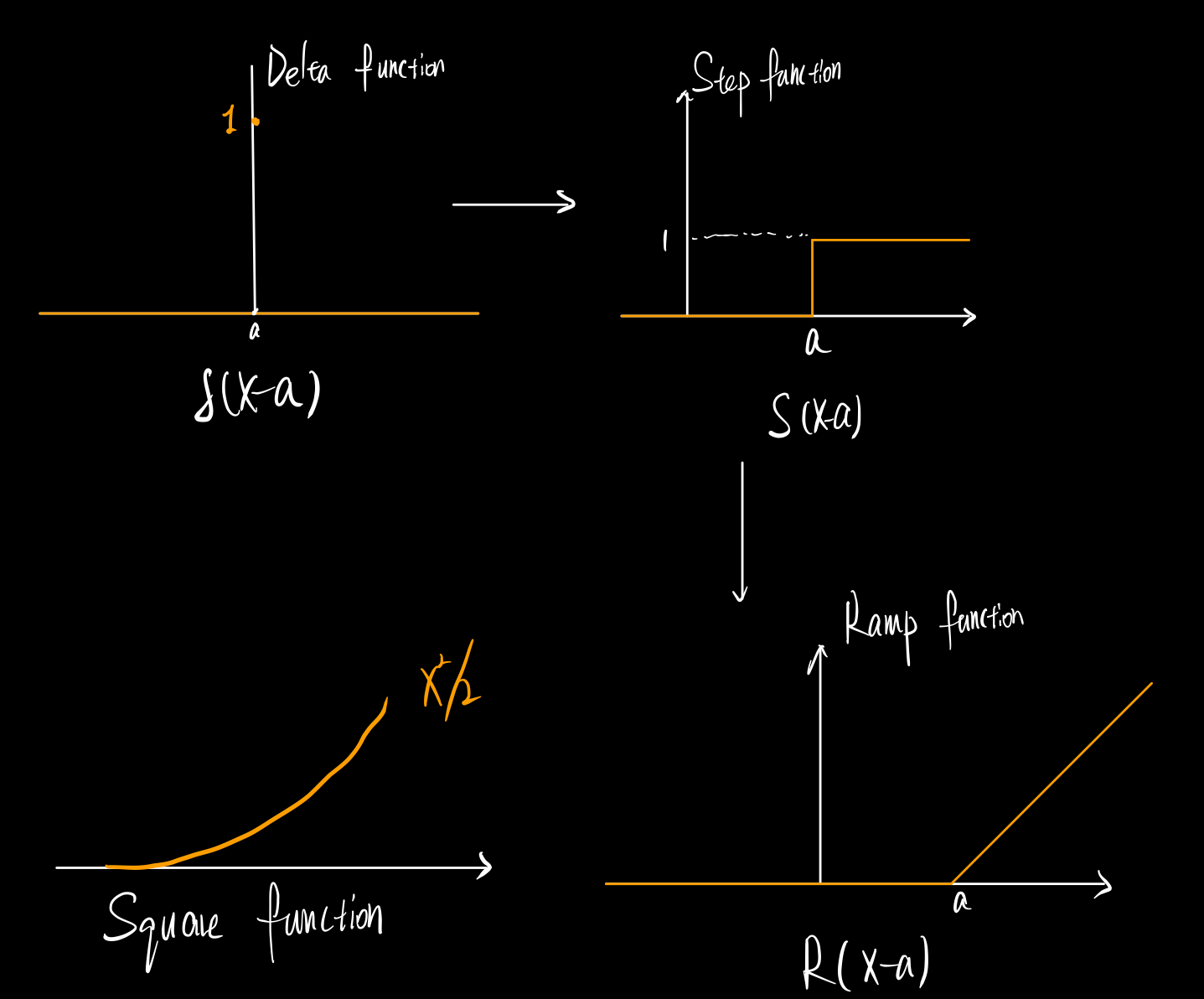
These funtions are "integral progressive". For exampple, the integration of delta function is the step function, the integration of step function is the Ramp function. And the are "differential progressive" reversely.

2. Bar Displacement

The model is, there is a stretchy bar, and we hang a load on it, and we want to calculate the displacement of each point of the bar.

2.1 Free-Free Case

The both ends of the bar are attached to "ground". And we can model this problem with differential equations. Since the load is attached at one point of the bar, the force on the bar can be described as a Delta function.

First, we can solve the problem solely with differential equation.

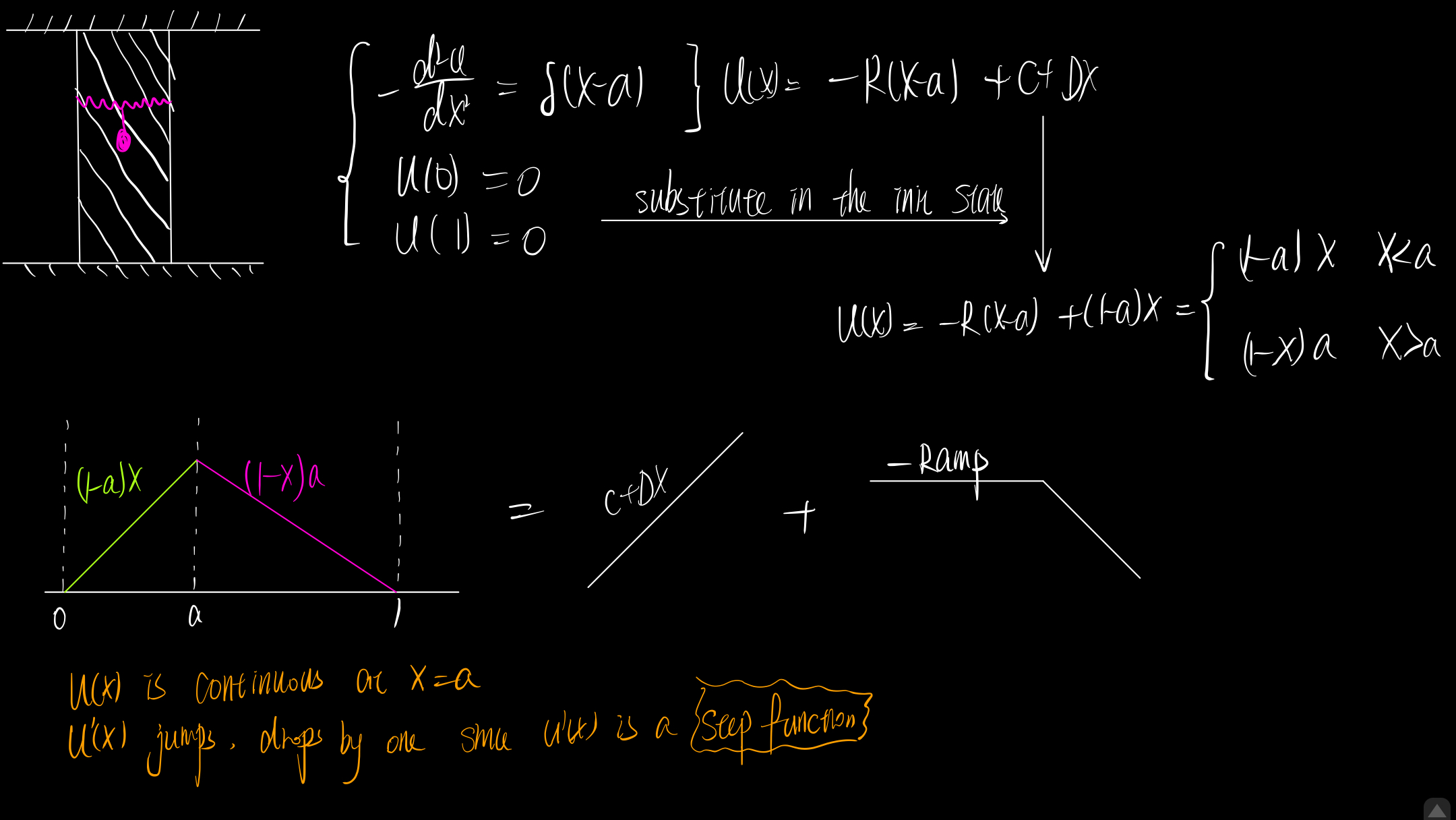
However, if we want to know only one or several points, solving a whole system with differential equation. Instead, we can solve the problem with simple matrix multiplication using our special matrix $K$.

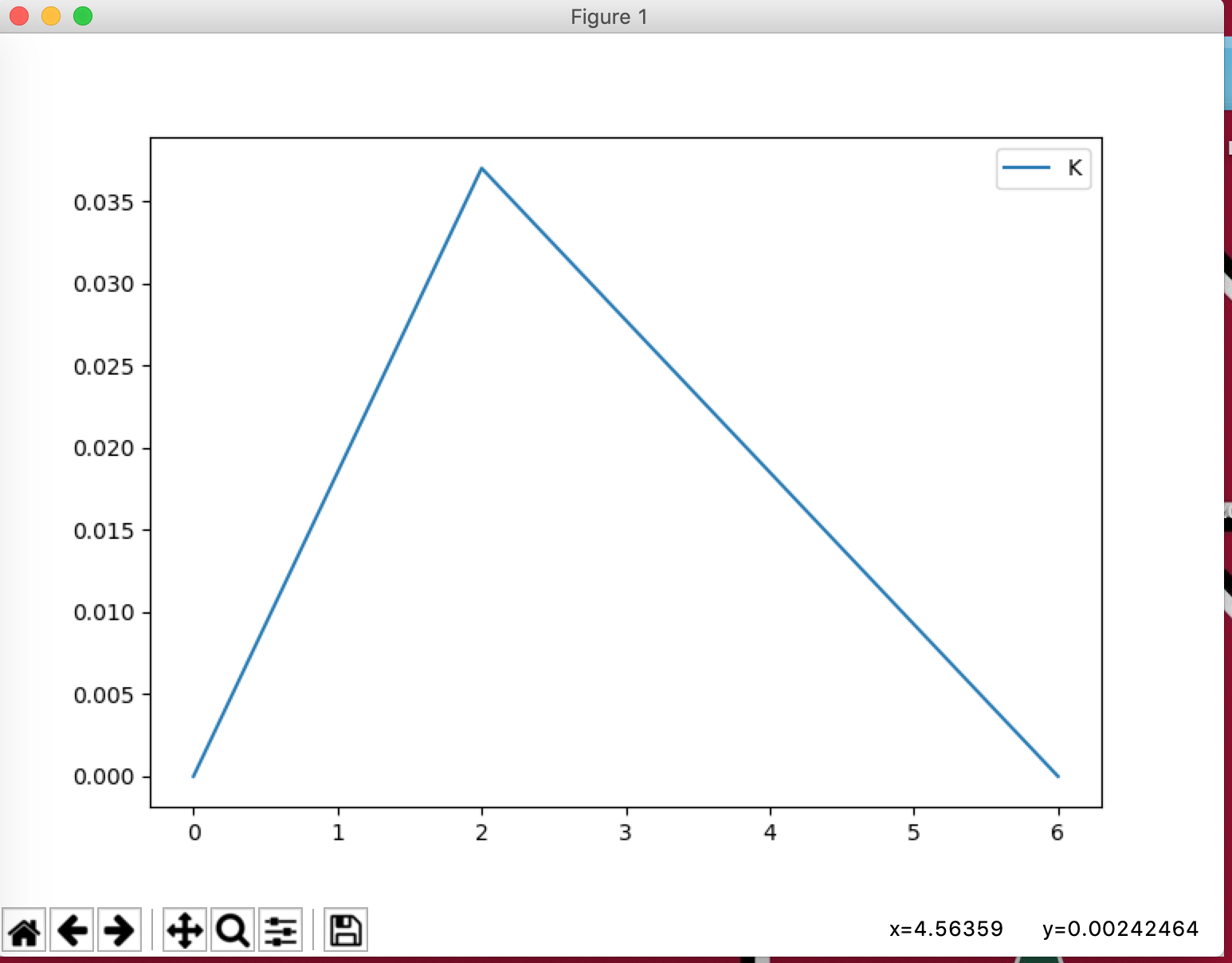
For example, the load is on the $2/5$ of the bar.

"""
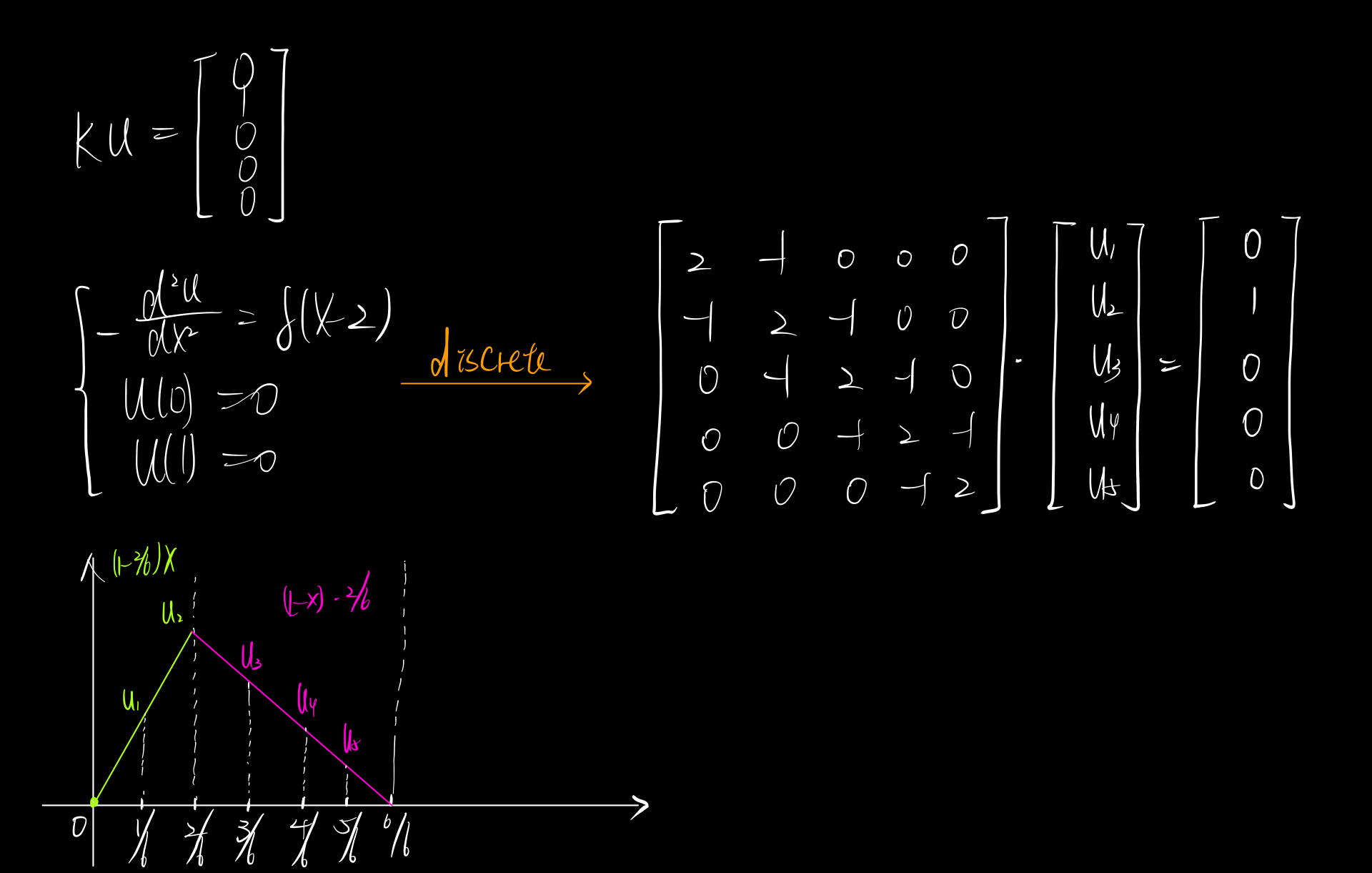
-u'' = alpha(x-2)
u(0) = 0
u(1) = 0
"""

K = np.array([
    [2, -1, 0, 0, 0],       # u1
    [-1, 2, -1, 0, 0],       # u2
    [0, -1, 2, -1, 0],       # u3
    [0, 0, -1, 2, -1],       # u4
    [0, 0, 0, -1, 2],        # u5
])      # Second-Order difference of Free-Free

force = np.array([0,1,0,0,0])
displacementK = (np.linalg.inv(K).dot(force) / 36).tolist()
displacementK = [0] + displacementK + [0]
plt.plot(displacementK, label="K")
plt.legend()
plt.show()

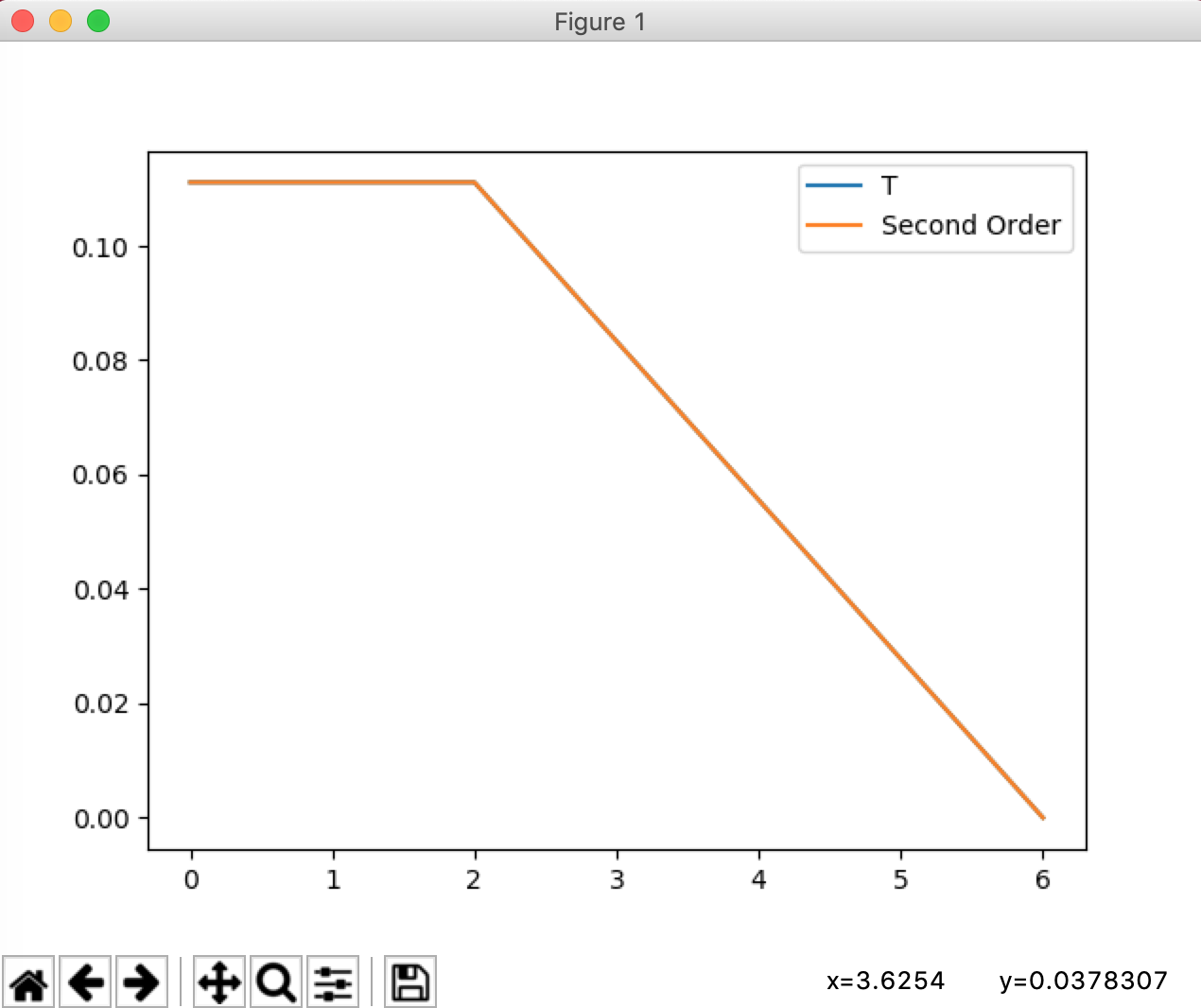
2.2 Free-Fixed

In free-fixed case, one end of the bar is attached to the "ground" while the other end is free, which means that the difference of displacement of the free end is 0. In mathematic formulas, $u'(0)=0$

"""
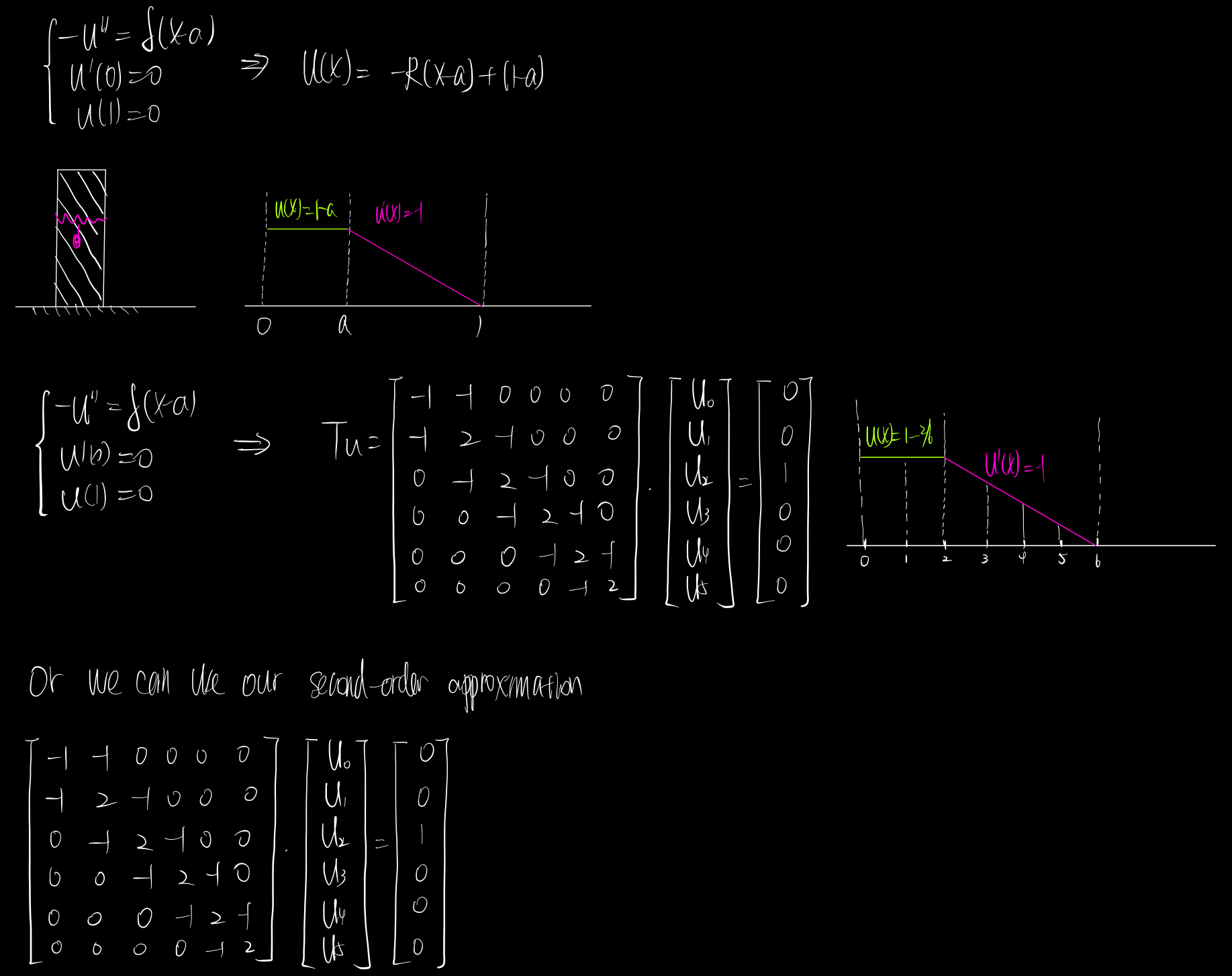
-u'' = alpha(x-2)
u'(0) = 0
u(1) = 0
"""
T = np.array([
    [1, -1, 0, 0, 0, 0],        # u0
    [-1, 2, -1, 0, 0, 0],       # u1
    [0, -1, 2, -1, 0, 0],       # u2
    [0, 0, -1, 2, -1, 0],       # u3
    [0, 0, 0, -1, 2, -1],       # u4
    [0, 0, 0, 0, -1, 2],        # u5
])     # First-order approximation for free-fixed


SecondOrder = np.array([
    [2, -2, 0, 0, 0, 0],        # u0
    [-1, 2, -1, 0, 0, 0],       # u1
    [0, -1, 2, -1, 0, 0],       # u2
    [0, 0, -1, 2, -1, 0],       # u3
    [0, 0, 0, -1, 2, -1],       # u4
    [0, 0, 0, 0, -1, 2],        # u5
])      # Second-order approximation for fre-fixed

force = np.array([0, 0, 1, 0, 0, 0])  # [u0, u1, u2, u3, u4, u5]


displacementT = (np.linalg.inv(T).dot(force) / 36).tolist() + [0]
displacementSecondOrder = (np.linalg.inv(SecondOrder).dot(force) / 36).tolist() + [0]

print(displacementT)
print(displacementSecondOrder)


plt.plot(displacementT, label="T")
plt.plot(displacementSecondOrder, label="Second Order")
plt.legend()
plt.show()